

Next: MEA Strukturen mit Penalty
Up: Praktikumsbericht RNA
Previous: Untersuchung Basenpaarlaenge mit Strukturanzahl
Nach dieser theoretischen Analyse wurde der Nussinov
Algorithmus[3] in der Zaehlvariante implementiert, um
damit die Anzahl der real moeglichen Strukturen zumindest etwas
genauer berechnen zu koennen. Auch hierbei musste wieder skaliert
werden, jedoch wurde hier im Log-Space des Logarithmus Naturalis
skaliert. Zusaetzlich wurde eine Vereinfachung genutzt, um Strukturen
ueber der zu berechnenden Basenpaardistanz zu berechnen. Hierzu wurde
die Sequenz schlicht verdoppelt und am Ende der ersten Haelfte um drei
NNN Basen erweitert, damit auch Basenpaare von Base 1 zu n moeglich
sind.
Zur Berechnung wird dadurch zwar mehr Speicher benoetigt und das fuellen der Matrix fuer die Strukturen dauert linear laenger, jedoch kann so auf weitere quadratische Berechnungen im Backtracking verzichten.
![$\displaystyle N[i,j] = \sum \begin{cases}N[i,j-1]\\ \sum_{i\le k \le j-1}{N[i,k-1] * 1 * N[k,j-1] * \sigma[k,j]} \end{cases}$](img40.png) |
(19) |
Die 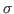 -Funktion testet hier immer, ob die momentane
Basenkombination real ueberhaupt paaren koennte und liefert
entsprechend dem Falle 1 oder 0 zurueck.
-Funktion testet hier immer, ob die momentane
Basenkombination real ueberhaupt paaren koennte und liefert
entsprechend dem Falle 1 oder 0 zurueck.
Das Backtracking erfolgte dann mittels:
![$\displaystyle C_m^d = \sum_{i=1}^{m-1}{\sum_{j=i+3}^m{ln(N[i+1,j-1]) * ln(N[j+1,(m*2+3)-1+2])}}$](img42.png) |
(20) |
Figure 10:
Nussinov Vorhersagen gegen theoretische
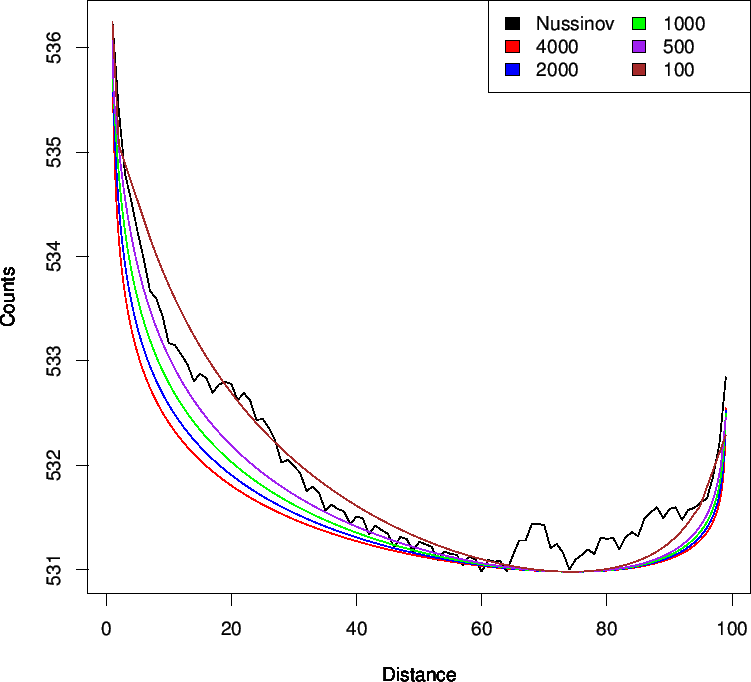 |


Next: MEA Strukturen mit Penalty
Up: Praktikumsbericht RNA
Previous: Untersuchung Basenpaarlaenge mit Strukturanzahl
Daniel Gerighausen
2013-07-19
![$\displaystyle N[i,j] = \sum \begin{cases}N[i,j-1]\\ \sum_{i\le k \le j-1}{N[i,k-1] * 1 * N[k,j-1] * \sigma[k,j]} \end{cases}$](img40.png)
![$\displaystyle N[i,j] = \sum \begin{cases}N[i,j-1]\\ \sum_{i\le k \le j-1}{N[i,k-1] * 1 * N[k,j-1] * \sigma[k,j]} \end{cases}$](img40.png)
![$\displaystyle C_m^d = \sum_{i=1}^{m-1}{\sum_{j=i+3}^m{ln(N[i+1,j-1]) * ln(N[j+1,(m*2+3)-1+2])}}$](img42.png)